There is a deep connection between mathematics and poetry. Fortunately, this mysterious link for mathematics and poetry lovers attracts practitioners of both disciplines and others to search for answers. In this book, we will be focusing on the connection between Sanskrit poetry and Mathematics.

Every single word is a combination of syllables. The stress of a syllable is the emphasis that falls on it when spoken. A "stressed" syllable is said LOUDER or with more emphasis than the other syllables in the word (assuming that the word has more than one syllable). Generally, short words like "a," "I," and "the" are not stressed. On the other hand, nouns and verbs (things and action words) are often stressed, even when they are just one syllable long. So, for example, words like "cat","ahead" and "jump" are stressed syllables.

An unstressed syllable is a syllable that is not emphasized in the word. Examples are "bite," "gang," and "blank." In poly-syllabic words, apart from one stressed syllable, all remaining syllables of the word are unstressed. However, we can't stress mono-syllabic words. We can only stress a syllable when it is more than one. A word basically has one stressed syllable and one or more unstressed syllables.

The arrangement of stresses within a poem is the foundation of poetic rhythm. The pattern of stressed and unstressed parts of words is known as the meter. It is the arrangement of words in regularly measured, patterned, or rhythmic lines or verses. Working out which syllables in a poem are stressed is known as scansion; once a metrical poem has been scanned, it should be possible to see the meter.

In Sanskrit poetry, stressed syllables are called long syllables, and unstressed syllables are called short syllables. A long syllable in Sanskrit is twice as long as a short syllable when you pronounce it. That is, when you read Sanskrit poetry, a long syllable lasts two beats of time, and a short syllable lasts one beat of time. Take the example of the Sanskrit word tattva. It is split as tat (long)-tva(short). If we distinctly enunciate each syllable, the first syllable's heaviness is unavoidable and lasts two beats of time.

In Sanskrit poetry, stressed syllables are called long syllables, and unstressed syllables are called short syllables. A long syllable in Sanskrit is twice as long as a short syllable when you pronounce it. That is, when you read Sanskrit poetry, a long syllable lasts two beats of time, and a short syllable lasts one beat of time. Take the example of the Sanskrit word tattva. It is split as tat (long)-tva(short). If we distinctly enunciate each syllable, the first syllable's heaviness is unavoidable and lasts two beats of time.

For example, a natural question that ancient Sanskrit poets were to ask when composing poetry is that a long syllable lasts two beats and a short syllable lasts one beat, so how many rhythms and poetic meters can one construct in six beats? These questions were raised even in 300 BC.

One possibility would be Long, Long, Long. Another would be Short, Short, Short......Short (six times), or you can mix them, say Short, Long, Long, Short, or Long, Long, Short, or Long, Long, Short, or Long, Long, Short, or Long, Long. So, what is the total number of ways you can fill six beats with longs and shorts?
We ask how many ways we can write the number n (n= 6 in our case ) as a sum of 1s and 2s where 1 is a short (takes one beat of time), and 2 is a long (takes two beats of time)

You can write 2 + 2 + 2 (=6 beats), which is the Long, Long, Long
or
1 + 1 + 1 +......+1 that is 6 shorts Or various combinations in between, with order mattering as it is poetry!

A way mathematician would approach the question in the same way that the poet would approach the question back in 300 BC: to work out the first few examples, understand the pattern, and formulate the theorem.
Suppose there is only one beat to fill; then there is only one way: a short (one beat).

If two beats, then we can have Long( 2 beat) or Short( 1 beat) Short (1 beat) so two ways

If you have three beats left, then you can do three Shorts or Long (2 beat) Short (1 beat), or you can do Short ( 1 beat) Long(2 beats), so 3 ways.

If you have four beats left, then four Shorts, Long, Short, Short in three different ways, or Two longs. Giving all together 5 ways. If you have five beats left, then five Shorts or Long, Short, Short, Short in four different ways, or Two Longs and a Short in 3 different ways. Giving all together 8 ways.
Finally, if you have six beats to fill, then you can have 6 Shorts or 3 Longs or 2 Longs and 2 Shorts in 6 different ways, or four Shorts and a Long in 5 different ways. Giving 13 different ways.

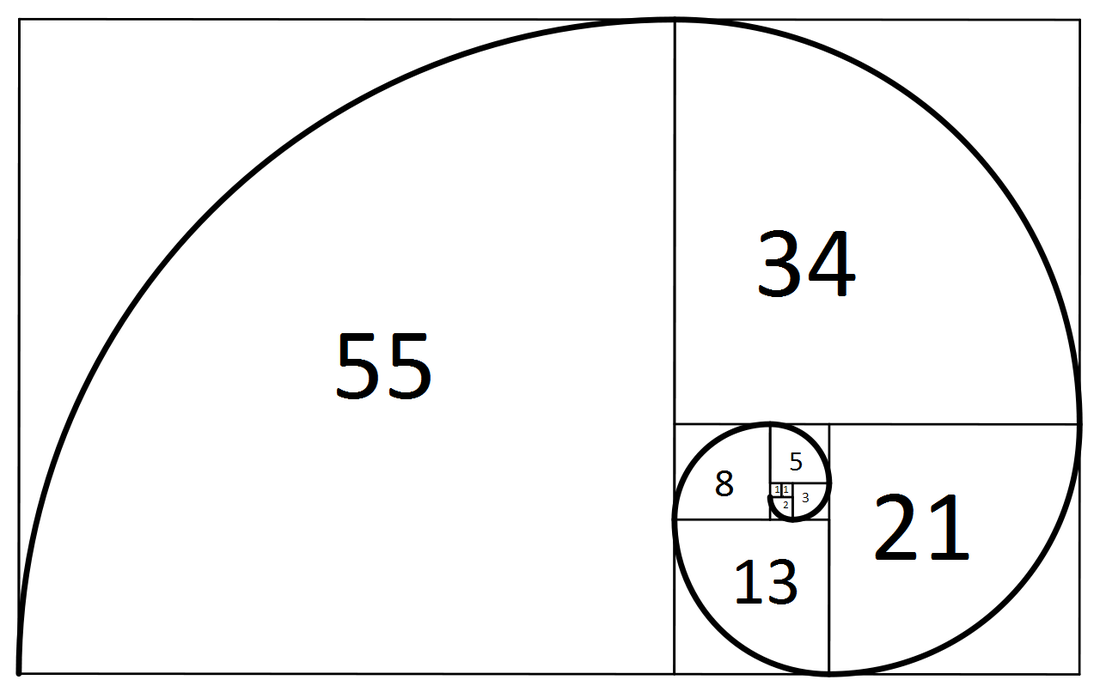
It is written in this beautiful Sanskrit poem translation, which says Write down numbers 1 and 2, and then every subsequent number you obtain should be by adding the two previous numbers.
Then, if you look at the nth number, that will give you the poetic meters of numbers having n beats,

1, 2, 3, 5, 8, 13, 21, 34, 55,..

The 6th number in this sequence corresponds to 13.

These are called the Virahanka numbers, after the linguist Virahanka (c. 700 A.D.), who first documented them and proved their recurrence property.
It is the first reference of these numbers that were first written about. Virahanka wrote about them in a complete way and also why these sequences gave the correct answers.

These numbers were also written about by Gopala (c.1135) and Hemachandra (c. 1150).

Of course, they are ubiquitously known as the Fibonacci numbers in the West after the Italian mathematician who wrote about them about 500 years later. So, Fibonacci was not even the first, second, or third person to discuss these numbers. Here is the irony of it all! Even in India, textbooks, math students, math teachers, and mathematicians call them the Fibonacci numbers!

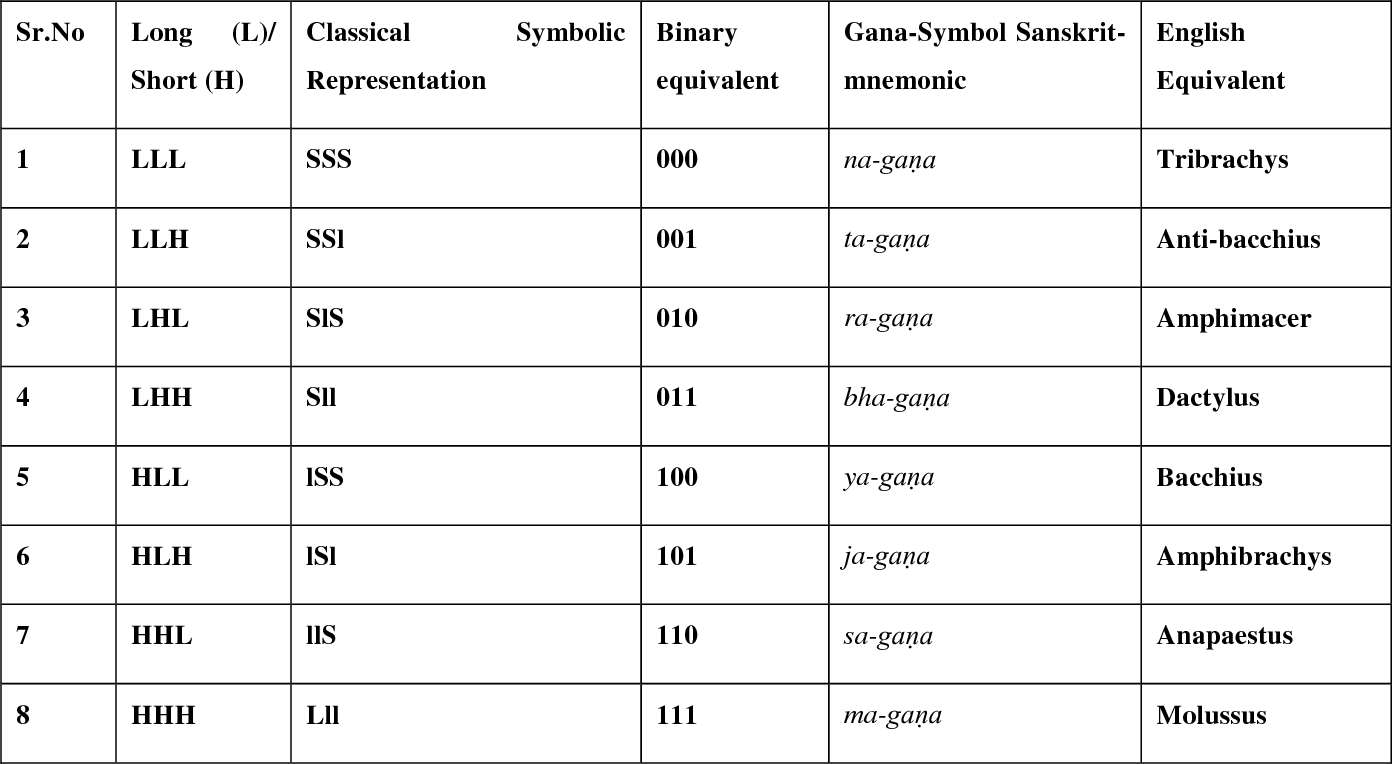
In classical poetic meters, particularly in quantitative meters like those found in Sanskrit poetry, the principle of equivalence is often observed. This means that two short syllables are considered equivalent to one long syllable in terms of metrical time.

In a short-long (1, 2) pattern, the total metrical time is distributed as follows:

Short syllable (1): 1 unit of time
Long syllable (2): 2 units of time
So, in a two-syllable pair (short-long), the total metrical time is 3 units.

If you have two pairs of short-long in a line, it would look like this: 1 2 1 2 1 2 1 2
Here, each pair contributes 3 units of time, and with four pairs, you get a total of 12 units of time, which is distributed across the 8 beats.
This principle of equivalence allows for flexibility in constructing metrical patterns while maintaining a consistent rhythmic structure.

Suppose we have 4 beats to fill. We can fill them as follows in 5 ways.

SSSS, LL, LSS, SLS, SSL
A possible rhythm could be
SSSS, LL, LSS, SLS, SSL
or LL, LSS, SLS, SSL, SSSS
or SSL, SLS, LSS, L.L., SSSS
and so on.

Therefore, we can create different Poetic rhythms by choosing various combinations of 4 beats (5 ways). This is how Sanskrit poets did it centuries ago!

PART VIII: Original poems written by me

The poetic metre followed:

As is shown in the analysis of the beats. There is a rhythm of short and long beats that are followed throughout my poem.

The pattern of 1-2-1-2 is repeated, occasionally interrupted with a "1-2" or a "1-1-2". Both of these meters are called "troachic" - an unstressed syllable followed by a stressed syllable and "iambic" meters - a stressed syllable followed by an unstressed syllable.